Szegedi Tudományegyetem - Ahol tudás és szándék találkozik
Tartalom
Tartalom átlépése.
Archívum
2009
6. szám - 2009. április 6.
Katedra
A matematikában a legnehezebb jól sejteni
2009
6. szám - 2009. április 6.
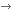Katedra
A matematikában a legnehezebb jól sejteniDacból kezdett matematikával foglalkozni, majd fizikusnak készült, végül mégis matematikus lett, bár saját bevallása szerint a mai napig elszámol dolgokat. Klukovits Lajos az elmúlt évtizedben főleg a matematika kultúrtörténetét kutatta, és úgy tűnik, kifogyhatatlan a több ezer éves matematikai érdekességekből.
Címkék: Katedra
Cikk nyomtatás
Link küldés
Megosztás
– A családjában több pedagógus is van. Ez a „hagyomány” indította el önt is a tanári pályán?
– Mind a négy nagyszülőm és két nagynéném is tanító vagy tanár volt. Anyai nagyapám a mostani SZTE Juhász Gyula Gyakorló Általános Iskola egyik elődjének matematika-természettan-ének-zene tanára volt, mellesleg amatőr orgonista. Édesanyám és apai nagyanyám egy időben Szeged-Alsóközpont (a mai Mórahalom) kissori iskolájában tanítottak, édesanyám később a községi iskolában. Bevallom, az 1950-60-as években nem tűnt megbecsültnek a tanár szakma. Nem is feltétlen akartam tanár lenni. Kezdetben fizikusnak készültem, de arról lebeszéltek, így 1963-ban jelentkeztem az akkor induló matematikus szakra. Mikor lediplomáztam, kaptam egy ajánlatot, hogy maradjak az egyetemen. Úgy látom, a mai napig nem értem fel a pedagógia magasságába, de ennek hiányát nem éreztem.
– Megtudhatjuk, ki és miért beszélte le a fizikáról?
– Elméleti fizikus akartam lenni, ám természettudományokban kevésbé jártas szüleim megijedtek, mi lesz velem. Édesapám elmesélte a szándékomat egy gimnáziumi ismerősének, Szalay Lászlónak (a biofizika tanszék megalapítójának). A tanár úr azt javasolta, előbb tanuljam meg tisztességesen a matematikát, utána legyek fizikus. De harmadéves matematikusként meghívtak az algebra tanszék kutató szemináriumára, és ez eldöntötte a sorsomat. Azért a matematika szakon is tíz féléven keresztül tanultam fizikát. Néha bánom, hogy nem lettem fizikus, de igazán érdekes dolgokat a kísérleti fizikusok csináltak, ám ahhoz nem volt se érzékem, se affinitásom.
– Kezdetektől az univerzális algebra érdekelte?
– Volt egy kis kitérő előtte. Ifjúkoromban egy dolgozat erejéig az automaták matematikai elméletéről írtam. Aztán Csákány Béla tanszékvezető urat akkoriban újra az univerzális algebra kezdte érdekelni. Felajánlotta, hogy válasszak a két terület között, és én az algebra mellett döntöttem.
– Hogyan kezdett a matematika kultúrtörténetével foglalkozni?
– Aspiránsként töltöttem hosszabb időt Németországban. Mikor hazajöttem, Pollák György tanár úr megunta a matematika történetének oktatását, de akkor még egy évig Szendrei Mária vette át a kurzust. Később a tanszékvezető úgy gondolta, úgyis sokat olvasok, jó lesz nekem ez a tantárgy. Eleinte rettentően nehéz volt: egy féléves kurzuson, heti két órában mit mondjak el négyezer év történetéből? Pollák tanár úr terelgetett, neki köszönhetem, hogy tisztességes általános műveltségre tettem szert. Sokat utaztunk együtt konferenciákra, és a hosszú út alatt Csákány Bélával felváltva szavaltak Arany-balladákat, én meg csak füleltem, mi mindent tudnak. Sajnos a középiskolai történelemoktatásban a hangsúly a királyokon és a háborúkon van. Szerintem a kultúra nem csak a humán kultúrából áll, ezért ha a „Fejezetek a matematika kultúrtörténetéből” című kurzuson Egyiptomhoz érünk, az istenek viselt dolgairól is beszélek, nem csak a Rhind-papiruszokról (óegyiptomi, számtannal és mértannal foglalkozó papirusztekercs, nevét Henry Rhind skót régiségkereskedőről kapta, aki sírrablóktól vásárolta meg, és a British Musem-nak ajándékozta – N. T.).
– Melyik a kedvenc része a matematika történetéből?
– Igazából nincs egy kedvenc részem. A legtöbb kultúrtörténeti publikációm az algebrához kapcsolódik. Nagy csodálója vagyok a görög matematikának. Archimédesz például korrektül kiszámolta a parabolaszelet területét, ami ma egy integrálszámítási feladat. Külön traktatusban írja le, hogyan jött rá, hogy mit kellene bizonyítania. Már pedig a matematikában a legnehezebb jól sejteni. Persze bizonyítani sem egyszerű, néha eltart pár száz évig, de az igazi nagy dolog jó sejtéseket megfogalmazni. De az ókori Mezopotámia algebrája is izgalmas. Hammurapi korában azzal az eljárással tudtak négyzetgyököt vonni, amelyet a mai számológépek is használnak. Az emögött álló algoritmus ugyanis tőlük származik. De a kora középkori iszlám világnak köszönhetjük, hogy rengeteg ókori görög és szanszkrit tudományos és filozófiai mű eljutott Európába. Az Ezeregy éjszaka meséiből ismert Hárún ar-Rashid ugyanis létező személy volt, aki alapított egy ugyanolyan intézményt, mint amilyen a Muszeion volt Alexandriában. Leginkább az a folyamat érdekel, hogyan zajlottak a matematika fejlődésének egyes lépései az ókor és a 20. század első harmadának vége között.
– Gondolja, hogy egyszer az önről elnevezett matematikai fogalmakat – „Klukovits-halmazt” és a „Klukovits-polinomot” – is tanítani fogják a „Fejezetek a matematika kultúrtörténetéből” című kurzuson?
– Nem hiszem, azok nagyon speciális dolgok. Számomra is véletlenül derült ki, hogy elneveztek rólam fogalmakat, amelyek az 1973-as egyetemi doktori értekezésem legmélyebb eredményére alapulnak. Ez mindössze egy ötoldalas cikk volt, egy akkor divatos jellemzési mód általánosításával jellemeztem az algebraosztályok ún. Hamilton-tulajdonságát. Az erre bevezetett polinomot nevezik olykor így.
Az 1990-es években derült ki, hogy több helyen is lehet alkalmazni. Az évtized végén kaptam egy amerikai folyóirattól egy vaskos cikket lektorálásra. Először majdnem visszautasítottam, majd mégis végigolvastam, és több helyen is megtaláltam benne a nevemet. Mondom: „Lajos, ez érdekes, ezt megnézzük, mégis csak az univerzális algebra nagymenői írták”. Egy nagy univerzálisalgebra-monográfiában is benne van az eredeti cikkem eredménye. Emiatt erre az írásomra sok hivatkozás van, bár akad, aki a monográfiára hivatkozva idézi az eredményemet. A matematikában nem lehet sokezres hivatkozási listát elérni, ezért ez az írásom ebből a szempontból kuriózum.
– Mi a véleménye a természettudományok jelenlegi középiskolai oktatásáról? Önnel hogyan szeretették meg a matematikát a gimnáziumban?
– Még az általános iskolában dacból kezdtem matematikával foglalkozni. Ötödik osztályban csak négyest kaptam matekból. Hozzátenném teljesen jogosan, a mai napig elszámolok dolgokat. Viszont a tanárom csak azokat akarta elengedni matekversenyre, akik ötöst kaptak. Ezen nagyon felmérgeltem magam, és nagyszájú gyerek lévén kiharcoltam, hogy én is indulhassak. Meg is nyertem a korosztályos és a városi versenyt is. Majd később a gimnáziumban egy idős tanárnő volt a matematikatanárom, aki azt mondta, a Középiskolai Matematikai és Fizikai Lapokban (KöMal) megjelent feladatok jó megoldásáért három ötöst ad. Gondoltam, úgyis elszámolnám a dolgozatokat, ez jó üzlet lesz nekem. A matematika szakos nagynéném egyik kolléganőjéhez jártam, ha elakadtam a feladatokban. Az ő férje villamosmérnök volt, aki egyszer azt mondta: „Lajos, foglalkozzunk egy kicsit a fizikapéldákkal is”. A KöMaL-ban dicséretekig jutottam. Később a gimnáziumban jó fizikatanárom is volt, így szerettem meg a fizikát.
Mi még sok kísérletet csináltunk az órákon. Egyszer átvittek minket a tanárképző főiskolára, ahol megmutatták, a hőmérséklet hogyan változtatja meg az anyagok tulajdonságait. Cseppfolyós levegőbe mártogattunk rózsát, ólomharangot, higanyt, és mi magunk bizonyosodhattunk meg róla, hogy a rózsát kalapáccsal alig lehetett széttörni, vagy hogy az ólomharang csengő hangon is tud szólni. Ezek örök emlékek maradtak. A mai gyerekeknek sokszor még egy ellenállást sem kell megmérniük fizika órán.
Az 1970-80-as években megreformálták a matematika és fizika oktatását. Akkor mondta Szőkefalvi-Nagy Béla – aki akkor az Akadémia matematikai bizottságának volt az elnöke –, hogy az új tankönyvek többségét be kellene zúzni, olyan rosszak. A lányom fizikakönyvét láttam, sokszor az alany és állítmány sem volt egyeztetve a szövegekben.
Szerencsére ott még nem tartunk, mint az az amerikai nő, aki a megfürdetett macskáját berakta a mikrohullámú sütőbe száradni. Még kártérítést is nyert, mondván, nem volt benne az eszköz használati utasításában, hogy nem lehet benne macskát szárítani.
A másik gond szerintem, hogy a tömegmédia felkapott több áltudományos dolgot: a horoszkóptól kezdve a feng shuiig vagy a távgyógyításig. Az emberek nem tudják elfogadni, hogy a természettudományok nem tudnak mindent megmagyarázni, és valószínűleg soha nem is fognak, hiszen az a tudomány halála lenne. De ettől még nem kell elhinni az energiaátvitelt.
Ráadásul a középiskolás matematikai anyag háromnegyede több ezer éves ismeretanyag, alig van benne olyan, ami modern kori matematika. Mindenféle furfangos szerkesztéseket kell csinálni, és fura egyenleteket megoldani. Minek? Mikor az emberek nem tudják, mi az a THM, és simán átverik őket. Nem látják át, hogyan számolhatják ki a biztosítók és a bankok olyan huncutul a kamatokat. Amerikai statisztikák szerint a matematikai pálya azért került a világ legkeresettebb foglalkozásai közé, mert a bank-biztosítói szféra felismerte, hasznos lehet számukra a matematikusok tudása. Ahogy korábban a termodinamikához értő fizikusokat is felismerte a tőzsde, ugyanis hasonló jellegű folyamatok játszódnak le mindkettőben. A középiskolában inkább egy speciális szemléletmódot kellene adni a diákoknak, absztrakciós készséget kellene kifejleszteni bennük, hogy meglássák a különböző területek összefüggéseit.
– Szegeden szerencsére mindig akadtak, akadnak kiemelkedő hallgatók.
– Szerencsére most is bőven vannak. A szegedi csapat a nemzetközi matematikaversenyeken rendszeresen bekerül az első háromba. De még az ELTE privilégiumaként számon tartott Schweitzer Miklós Matematikai Emlékversenyen is nyert már szegedi hallgató. E versenyeken matematikus szakos hallgatók indulnak. Egyik tanári szakirányos hallgatóm, Kulcsár Nárcisz is kiemelkedőnek tekinthető diákunk. A második kultúrtörténeti kurzusomat vette fel ebben a félévben, közben derült ki, hogy ő az egyetemi matematika szak mellett rajz szakos is a tanárképző karon. Nagyon lelkesen és teljesen önállóan szedi össze az anyagot a diplomamunkájához, amit reneszánsz festészetelmélet matematikai összefüggéseiről ír. Nagyon érdekes és izgalmas téma!
– Hol áll a Bolyai Intézet a nemzetközi matematikai porondon?
– Ahogy az irodalom és a történelem, a matematika is nagyon szerteágazó lett. Gauss, Hilbert és talán Neumann János volt az utolsó, aki átlátta a matematikát. A matematikán belül több részterületen is a világ elitjébe tartoznak a szegedi matematikusok. Például az univerzális algebra négy fellegvárának egyikeként emlegetik Szegedet.
– 2000 óta az SZTE Doktori Intézet igazgatója. Hogy áll Szeged a doktori iskolákkal?
– Szegeden tizenkilenc doktori iskola van és több mint nyolcszáz PhD-hallgató, akiknek a zömét a TTIK és az ÁOK adja. A legfrissebb a filozófiai és az informatikai doktori iskola, s jelenleg dolgozunk Kerek Ferenc dékán úrral egy DLA (Doctor of Liberal Arts) képzésen a zenészek számára.
– Mivel foglalkozik egy matematikus a szabadidejében?
– Amivel minden magát műveltnek tartó ember – olvasással. Sajnos egyre kevesebb időm van rá, de igyekszem. Tízéves koromtól kezdve fényképezgetek is, most már digitálisan, de időnként az analóg képkidolgozásba is belefolyok. Szeretek jó időben friss levegőn kertészkedni, gyümölcstermesztéssel foglalkozom, és pálinkához cefrét erjesztek, részint szőlőből, részint más gyümölcsökből. A permetezés az én feladatom a családban, de kapálni nem szeretek. A jó bort is nagyon tisztelem és szeretem, folyamatosan művelődöm a bor kultúrájából is. Korábban kosárlabdáztam és atlétikáztam, de a térdem nem bírta. Az atlétikában voltam eredményesebb, de a kosárlabdát szerettem jobban, az nem volt olyan „napszámos jellegű”. Ma már csak biciklizgetek, van, hogy napi fél órát a lakásban is tekerek a szobabiciklin. Ezt hívom én „öregedő ember egészségmegőrző kúrájának”.
– Mind a négy nagyszülőm és két nagynéném is tanító vagy tanár volt. Anyai nagyapám a mostani SZTE Juhász Gyula Gyakorló Általános Iskola egyik elődjének matematika-természettan-ének-zene tanára volt, mellesleg amatőr orgonista. Édesanyám és apai nagyanyám egy időben Szeged-Alsóközpont (a mai Mórahalom) kissori iskolájában tanítottak, édesanyám később a községi iskolában. Bevallom, az 1950-60-as években nem tűnt megbecsültnek a tanár szakma. Nem is feltétlen akartam tanár lenni. Kezdetben fizikusnak készültem, de arról lebeszéltek, így 1963-ban jelentkeztem az akkor induló matematikus szakra. Mikor lediplomáztam, kaptam egy ajánlatot, hogy maradjak az egyetemen. Úgy látom, a mai napig nem értem fel a pedagógia magasságába, de ennek hiányát nem éreztem.
 |
Klukovits Lajos 1944-ben született Szegeden, a Radnóti Miklós Gimnáziumban érettségizett 1963-ban. 1968-ban szerzett diplomát a szegedi József Attila Tudományegyetem matematikus szakán. 1973-ban egyetemi doktori, 1987-ben kandidátusi fokozatot szerzett. Ösztöndíjas gyakornok, majd tanársegéd, adjunktus, docens a JATE (majd az SZTE) Bolyai Intézete Algebra és Számelmélet Tanszékén. Kutatómunkát az univerzális (általános) algebra területén folytat, de az utóbbi években az érdeklődése egyre inkább a matematika kultúrtörténete felé fordult. Kezdetben a régi JATE, majd 2000-től az SZTE Doktori Iskola igazgatója. 2009-ben megkapta a Magyar Köztársasági Érdemrend lovagkeresztjét. Fotó: Segesvári Csaba |
|---|
– Megtudhatjuk, ki és miért beszélte le a fizikáról?
– Elméleti fizikus akartam lenni, ám természettudományokban kevésbé jártas szüleim megijedtek, mi lesz velem. Édesapám elmesélte a szándékomat egy gimnáziumi ismerősének, Szalay Lászlónak (a biofizika tanszék megalapítójának). A tanár úr azt javasolta, előbb tanuljam meg tisztességesen a matematikát, utána legyek fizikus. De harmadéves matematikusként meghívtak az algebra tanszék kutató szemináriumára, és ez eldöntötte a sorsomat. Azért a matematika szakon is tíz féléven keresztül tanultam fizikát. Néha bánom, hogy nem lettem fizikus, de igazán érdekes dolgokat a kísérleti fizikusok csináltak, ám ahhoz nem volt se érzékem, se affinitásom.
– Kezdetektől az univerzális algebra érdekelte?
– Volt egy kis kitérő előtte. Ifjúkoromban egy dolgozat erejéig az automaták matematikai elméletéről írtam. Aztán Csákány Béla tanszékvezető urat akkoriban újra az univerzális algebra kezdte érdekelni. Felajánlotta, hogy válasszak a két terület között, és én az algebra mellett döntöttem.
Hammurapi és a négyzetgyök
– Hogyan kezdett a matematika kultúrtörténetével foglalkozni?
– Aspiránsként töltöttem hosszabb időt Németországban. Mikor hazajöttem, Pollák György tanár úr megunta a matematika történetének oktatását, de akkor még egy évig Szendrei Mária vette át a kurzust. Később a tanszékvezető úgy gondolta, úgyis sokat olvasok, jó lesz nekem ez a tantárgy. Eleinte rettentően nehéz volt: egy féléves kurzuson, heti két órában mit mondjak el négyezer év történetéből? Pollák tanár úr terelgetett, neki köszönhetem, hogy tisztességes általános műveltségre tettem szert. Sokat utaztunk együtt konferenciákra, és a hosszú út alatt Csákány Bélával felváltva szavaltak Arany-balladákat, én meg csak füleltem, mi mindent tudnak. Sajnos a középiskolai történelemoktatásban a hangsúly a királyokon és a háborúkon van. Szerintem a kultúra nem csak a humán kultúrából áll, ezért ha a „Fejezetek a matematika kultúrtörténetéből” című kurzuson Egyiptomhoz érünk, az istenek viselt dolgairól is beszélek, nem csak a Rhind-papiruszokról (óegyiptomi, számtannal és mértannal foglalkozó papirusztekercs, nevét Henry Rhind skót régiségkereskedőről kapta, aki sírrablóktól vásárolta meg, és a British Musem-nak ajándékozta – N. T.).
– Melyik a kedvenc része a matematika történetéből?
– Igazából nincs egy kedvenc részem. A legtöbb kultúrtörténeti publikációm az algebrához kapcsolódik. Nagy csodálója vagyok a görög matematikának. Archimédesz például korrektül kiszámolta a parabolaszelet területét, ami ma egy integrálszámítási feladat. Külön traktatusban írja le, hogyan jött rá, hogy mit kellene bizonyítania. Már pedig a matematikában a legnehezebb jól sejteni. Persze bizonyítani sem egyszerű, néha eltart pár száz évig, de az igazi nagy dolog jó sejtéseket megfogalmazni. De az ókori Mezopotámia algebrája is izgalmas. Hammurapi korában azzal az eljárással tudtak négyzetgyököt vonni, amelyet a mai számológépek is használnak. Az emögött álló algoritmus ugyanis tőlük származik. De a kora középkori iszlám világnak köszönhetjük, hogy rengeteg ókori görög és szanszkrit tudományos és filozófiai mű eljutott Európába. Az Ezeregy éjszaka meséiből ismert Hárún ar-Rashid ugyanis létező személy volt, aki alapított egy ugyanolyan intézményt, mint amilyen a Muszeion volt Alexandriában. Leginkább az a folyamat érdekel, hogyan zajlottak a matematika fejlődésének egyes lépései az ókor és a 20. század első harmadának vége között.
„Klukovits-halmaz” és a „Klukovits-polinom”
– Gondolja, hogy egyszer az önről elnevezett matematikai fogalmakat – „Klukovits-halmazt” és a „Klukovits-polinomot” – is tanítani fogják a „Fejezetek a matematika kultúrtörténetéből” című kurzuson?
– Nem hiszem, azok nagyon speciális dolgok. Számomra is véletlenül derült ki, hogy elneveztek rólam fogalmakat, amelyek az 1973-as egyetemi doktori értekezésem legmélyebb eredményére alapulnak. Ez mindössze egy ötoldalas cikk volt, egy akkor divatos jellemzési mód általánosításával jellemeztem az algebraosztályok ún. Hamilton-tulajdonságát. Az erre bevezetett polinomot nevezik olykor így.
Az 1990-es években derült ki, hogy több helyen is lehet alkalmazni. Az évtized végén kaptam egy amerikai folyóirattól egy vaskos cikket lektorálásra. Először majdnem visszautasítottam, majd mégis végigolvastam, és több helyen is megtaláltam benne a nevemet. Mondom: „Lajos, ez érdekes, ezt megnézzük, mégis csak az univerzális algebra nagymenői írták”. Egy nagy univerzálisalgebra-monográfiában is benne van az eredeti cikkem eredménye. Emiatt erre az írásomra sok hivatkozás van, bár akad, aki a monográfiára hivatkozva idézi az eredményemet. A matematikában nem lehet sokezres hivatkozási listát elérni, ezért ez az írásom ebből a szempontból kuriózum.
– Mi a véleménye a természettudományok jelenlegi középiskolai oktatásáról? Önnel hogyan szeretették meg a matematikát a gimnáziumban?
– Még az általános iskolában dacból kezdtem matematikával foglalkozni. Ötödik osztályban csak négyest kaptam matekból. Hozzátenném teljesen jogosan, a mai napig elszámolok dolgokat. Viszont a tanárom csak azokat akarta elengedni matekversenyre, akik ötöst kaptak. Ezen nagyon felmérgeltem magam, és nagyszájú gyerek lévén kiharcoltam, hogy én is indulhassak. Meg is nyertem a korosztályos és a városi versenyt is. Majd később a gimnáziumban egy idős tanárnő volt a matematikatanárom, aki azt mondta, a Középiskolai Matematikai és Fizikai Lapokban (KöMal) megjelent feladatok jó megoldásáért három ötöst ad. Gondoltam, úgyis elszámolnám a dolgozatokat, ez jó üzlet lesz nekem. A matematika szakos nagynéném egyik kolléganőjéhez jártam, ha elakadtam a feladatokban. Az ő férje villamosmérnök volt, aki egyszer azt mondta: „Lajos, foglalkozzunk egy kicsit a fizikapéldákkal is”. A KöMaL-ban dicséretekig jutottam. Később a gimnáziumban jó fizikatanárom is volt, így szerettem meg a fizikát.
Mi még sok kísérletet csináltunk az órákon. Egyszer átvittek minket a tanárképző főiskolára, ahol megmutatták, a hőmérséklet hogyan változtatja meg az anyagok tulajdonságait. Cseppfolyós levegőbe mártogattunk rózsát, ólomharangot, higanyt, és mi magunk bizonyosodhattunk meg róla, hogy a rózsát kalapáccsal alig lehetett széttörni, vagy hogy az ólomharang csengő hangon is tud szólni. Ezek örök emlékek maradtak. A mai gyerekeknek sokszor még egy ellenállást sem kell megmérniük fizika órán.
Az 1970-80-as években megreformálták a matematika és fizika oktatását. Akkor mondta Szőkefalvi-Nagy Béla – aki akkor az Akadémia matematikai bizottságának volt az elnöke –, hogy az új tankönyvek többségét be kellene zúzni, olyan rosszak. A lányom fizikakönyvét láttam, sokszor az alany és állítmány sem volt egyeztetve a szövegekben.
Szerencsére ott még nem tartunk, mint az az amerikai nő, aki a megfürdetett macskáját berakta a mikrohullámú sütőbe száradni. Még kártérítést is nyert, mondván, nem volt benne az eszköz használati utasításában, hogy nem lehet benne macskát szárítani.
A másik gond szerintem, hogy a tömegmédia felkapott több áltudományos dolgot: a horoszkóptól kezdve a feng shuiig vagy a távgyógyításig. Az emberek nem tudják elfogadni, hogy a természettudományok nem tudnak mindent megmagyarázni, és valószínűleg soha nem is fognak, hiszen az a tudomány halála lenne. De ettől még nem kell elhinni az energiaátvitelt.
Ráadásul a középiskolás matematikai anyag háromnegyede több ezer éves ismeretanyag, alig van benne olyan, ami modern kori matematika. Mindenféle furfangos szerkesztéseket kell csinálni, és fura egyenleteket megoldani. Minek? Mikor az emberek nem tudják, mi az a THM, és simán átverik őket. Nem látják át, hogyan számolhatják ki a biztosítók és a bankok olyan huncutul a kamatokat. Amerikai statisztikák szerint a matematikai pálya azért került a világ legkeresettebb foglalkozásai közé, mert a bank-biztosítói szféra felismerte, hasznos lehet számukra a matematikusok tudása. Ahogy korábban a termodinamikához értő fizikusokat is felismerte a tőzsde, ugyanis hasonló jellegű folyamatok játszódnak le mindkettőben. A középiskolában inkább egy speciális szemléletmódot kellene adni a diákoknak, absztrakciós készséget kellene kifejleszteni bennük, hogy meglássák a különböző területek összefüggéseit.
Szegediek a nemzetközi élmezőnyben
– Szegeden szerencsére mindig akadtak, akadnak kiemelkedő hallgatók.
– Szerencsére most is bőven vannak. A szegedi csapat a nemzetközi matematikaversenyeken rendszeresen bekerül az első háromba. De még az ELTE privilégiumaként számon tartott Schweitzer Miklós Matematikai Emlékversenyen is nyert már szegedi hallgató. E versenyeken matematikus szakos hallgatók indulnak. Egyik tanári szakirányos hallgatóm, Kulcsár Nárcisz is kiemelkedőnek tekinthető diákunk. A második kultúrtörténeti kurzusomat vette fel ebben a félévben, közben derült ki, hogy ő az egyetemi matematika szak mellett rajz szakos is a tanárképző karon. Nagyon lelkesen és teljesen önállóan szedi össze az anyagot a diplomamunkájához, amit reneszánsz festészetelmélet matematikai összefüggéseiről ír. Nagyon érdekes és izgalmas téma!
– Hol áll a Bolyai Intézet a nemzetközi matematikai porondon?
– Ahogy az irodalom és a történelem, a matematika is nagyon szerteágazó lett. Gauss, Hilbert és talán Neumann János volt az utolsó, aki átlátta a matematikát. A matematikán belül több részterületen is a világ elitjébe tartoznak a szegedi matematikusok. Például az univerzális algebra négy fellegvárának egyikeként emlegetik Szegedet.
– 2000 óta az SZTE Doktori Intézet igazgatója. Hogy áll Szeged a doktori iskolákkal?
– Szegeden tizenkilenc doktori iskola van és több mint nyolcszáz PhD-hallgató, akiknek a zömét a TTIK és az ÁOK adja. A legfrissebb a filozófiai és az informatikai doktori iskola, s jelenleg dolgozunk Kerek Ferenc dékán úrral egy DLA (Doctor of Liberal Arts) képzésen a zenészek számára.
| TUDTA |
|---|
| Fibonacci (Leonrado di Pisa) olasz matematikus is mecsetiskolákban, arab matematikusoktól tanult. ő terjesztette el az arab számokat Európában. Ám a Fibonacci-sorozatot nem ő fedezte fel, csak példaként használta egyik művében – meséli Klukovits Lajos. A sorozat lényege: az első két elem a 1 és az 1, a további elemeket pedig az előző kettő összegeként kapjuk meg, azaz: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 stb. Minél későbbi tagjait vesszük a sorozatnak, két egymást követő szám aránya annál inkább az aranymetszéshez fog közelíteni. Az irodalomban ez A Da Vinci-kód című regényben kapott fontos szerepet. A számsorozat a természetben is megfigyelhető, a virágszirmok száma gyakran Fibonacci-szám (például egyes százszorszépfajoknak 34, 55, 89 darab szirmuk van), de a zenében is használják néha hangolásra. |
– Mivel foglalkozik egy matematikus a szabadidejében?
– Amivel minden magát műveltnek tartó ember – olvasással. Sajnos egyre kevesebb időm van rá, de igyekszem. Tízéves koromtól kezdve fényképezgetek is, most már digitálisan, de időnként az analóg képkidolgozásba is belefolyok. Szeretek jó időben friss levegőn kertészkedni, gyümölcstermesztéssel foglalkozom, és pálinkához cefrét erjesztek, részint szőlőből, részint más gyümölcsökből. A permetezés az én feladatom a családban, de kapálni nem szeretek. A jó bort is nagyon tisztelem és szeretem, folyamatosan művelődöm a bor kultúrájából is. Korábban kosárlabdáztam és atlétikáztam, de a térdem nem bírta. Az atlétikában voltam eredményesebb, de a kosárlabdát szerettem jobban, az nem volt olyan „napszámos jellegű”. Ma már csak biciklizgetek, van, hogy napi fél órát a lakásban is tekerek a szobabiciklin. Ezt hívom én „öregedő ember egészségmegőrző kúrájának”.
Nagy Timea
Címkék
Katedra ,
Legolvasottabb
Portál
Hírek, aktualitások 
Rendezvénynaptár
-
Karikó Katalin állandó kiállítás
január 06. - június 02. -
Szorgalmi időszak
február 10. - május 24. -
Szorgalmi időszak
február 10. - május 24. -
Szorgalmi időszak
február 10. - május 24. -
Szorgalmi időszak
február 10. - május 24.
Gyorslinkek
Lábléc
Szegedi Tudományegyetem
6720 Szeged, Dugonics tér 13.
Központi telefonszám: (+36-62) 544-000
Központi fax: (+36-62) 546-371
© 2014 Szegedi Tudományegyetem. Minden jog fenntartva.
A Szegedi Tudományegyetem internet kapcsolatát az 
biztosítja