Szegedi Tudományegyetem - Ahol tudás és szándék találkozik
Tartalom
Tartalom átlépése.
Archívum
 2010
2010
 5. szám - 2010. március 29.
5. szám - 2010. március 29.
 Szabadegyetem
Szabadegyetem
 Lehetetlen?!
Lehetetlen?!
Ezt követően a geometriai szerkesztéshez kapcsolódva három görög problémával ismerkedhettünk meg. Az első példa a kockakettőzés volt, amely a legenda szerint Délosz szigetéről származik. Pestisjárvány tombolt a szigeten, és az emberek a déloszi jósdához fordultak segítségül, ahol megtudták, hogy azzal csillapíthatják le az istenek haragját, ha a kocka alakú oltárt a kétszeresére növelik. Mindezt úgy, hogy az oltár térfogatát duplázzák meg csupán körző és vonalzó segítségével. A feladat „megoldása” azonban bebizonyította, hogy a kockakettőzés körzővel és vonalzóval lehetetlen.
A második példa a szögharmadolás problematikája volt, ahol a végén szintén bebizonyosodott, hogy a szögharmadolás is lehetetlen körzővel és vonalzóval. Ezt Pierre Laurent Wanztel (1814-1848) francia matematikus bizonyította be 1837-ben.
A harmadik görög probléma a kör négyszögesítése. A feladat itt pontosan az, hogy egy adott, mondjuk egységsugarú körhöz kell megszerkeszteni annak a négyzetnek az oldalát, amelynek a területe megegyezik az adott kör területével. Ennek lehetetlenségét (azaz, hogy ennek szerkesztése körzővel és vonalzóval lehetetlen) 1882-ben Ferdinand Lindemann német matematikus igazolta.
Az előadás második része megismertette a leghíresebb magyar és külföldi eredményeket. A magyarok esetében Bolyai János nevéhez kötődik ez a dicsőség, aki megalapozta a nemeuklideszi geometriát. Ahogy ő fogalmazott: „A semmiből egy új, más világot teremtettem.”
A leghíresebb matematikai eredmény pedig a Fermat-sej-téshez kapcsolódik, ami a következő: „Lehetetlen egy köbszámot felírni két köbszám összegeként, [...], általában lehetetlen bármely magasabb hatványt felírni két ugyanolyan hatvány összegeként, igazán csodálatos bizonyítást találtam erre a tételre. A margó azonban túlságosan keskeny, semhogy ideírhatnám…” Végül 1995-ben Andrew Wiles bizonyította be a Fermat által a 17. században csupán csak sejtetett lehetetlent.
Az is kiderült előadáson, hogy a lehetetlen bizony hasznos is lehet. Azt tudjuk, hogy minden szám felírható prímszámok szorzataként. (A prímszámok olyan számok, melyek nem írhatók fel két szám szorzataként, például: 17,23, 29.) Ugyanakkor lehetetlen gyorsan megtalálni a számok prímtényezőit, ami felhasználható arra, hogy nyitott csatornán (például interneten) titkos adatokat kódolva továbbítsunk. Ezt az eljárást tesztelték is azzal, hogy nagyon nehéz számokat adtak meg, és aki ezeket megfejtette (megtalálta a prímtényezőket), az pénzjutalomban részesült. Mindemellett ezzel bebizonyították, hogy ez a rendszer elég biztonságos, legalábbis jelenleg.
Az óra harmadik részében megismertük a Banach–Tarski-paradoxont, s arra is fény derült, ami valószínűleg sokak fantáziáját megmozgatja és kedélyét felborzolja, hogy még a demokrácia is lehetetlen...
 2010
2010
 5. szám - 2010. március 29.
5. szám - 2010. március 29.
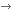 Szabadegyetem
Szabadegyetem
 Lehetetlen?!
Lehetetlen?!A matematikai bizonyításoknak bizony se végük, se hosszuk, de azt nem sokan gondolnák, hogy a matematikában még a lehetetlen is igazolható. Totik Vilmos akadémikus március 24-én a Szabadegyetemen számos szemléletes példával bizonyította, hogy igenis a lehetetlent is lehet igazolni.
Címkék: Szabadegyetem
Az SZTE TTIK Bolyai Intézet tanszékvezető egyetemi tanárának előadása sorozatos rejtvények és fejtörők segítségével, illetve azok matematikai magyarázataival bizonyította a lehetetlent. Felmerült Leonard Euler neve és a königsbergi hidak példája, valamint ezzel a síkba rajzolhatóság problémája is. Erre a kérdésére Kuratowski tétele adja meg a választ, miszerint egy alakzat pontosan akkor rajzolható le a síkban, ha nem tartalmazza a 3 ház, 3 kút alakzatot, illetve a teljes ötszöget.
| Totik Vilmos: A lehetetlen hasznos is lehet. |
A második példa a szögharmadolás problematikája volt, ahol a végén szintén bebizonyosodott, hogy a szögharmadolás is lehetetlen körzővel és vonalzóval. Ezt Pierre Laurent Wanztel (1814-1848) francia matematikus bizonyította be 1837-ben.
A harmadik görög probléma a kör négyszögesítése. A feladat itt pontosan az, hogy egy adott, mondjuk egységsugarú körhöz kell megszerkeszteni annak a négyzetnek az oldalát, amelynek a területe megegyezik az adott kör területével. Ennek lehetetlenségét (azaz, hogy ennek szerkesztése körzővel és vonalzóval lehetetlen) 1882-ben Ferdinand Lindemann német matematikus igazolta.
Az előadás második része megismertette a leghíresebb magyar és külföldi eredményeket. A magyarok esetében Bolyai János nevéhez kötődik ez a dicsőség, aki megalapozta a nemeuklideszi geometriát. Ahogy ő fogalmazott: „A semmiből egy új, más világot teremtettem.”
A leghíresebb matematikai eredmény pedig a Fermat-sej-téshez kapcsolódik, ami a következő: „Lehetetlen egy köbszámot felírni két köbszám összegeként, [...], általában lehetetlen bármely magasabb hatványt felírni két ugyanolyan hatvány összegeként, igazán csodálatos bizonyítást találtam erre a tételre. A margó azonban túlságosan keskeny, semhogy ideírhatnám…” Végül 1995-ben Andrew Wiles bizonyította be a Fermat által a 17. században csupán csak sejtetett lehetetlent.
Az is kiderült előadáson, hogy a lehetetlen bizony hasznos is lehet. Azt tudjuk, hogy minden szám felírható prímszámok szorzataként. (A prímszámok olyan számok, melyek nem írhatók fel két szám szorzataként, például: 17,23, 29.) Ugyanakkor lehetetlen gyorsan megtalálni a számok prímtényezőit, ami felhasználható arra, hogy nyitott csatornán (például interneten) titkos adatokat kódolva továbbítsunk. Ezt az eljárást tesztelték is azzal, hogy nagyon nehéz számokat adtak meg, és aki ezeket megfejtette (megtalálta a prímtényezőket), az pénzjutalomban részesült. Mindemellett ezzel bebizonyították, hogy ez a rendszer elég biztonságos, legalábbis jelenleg.
Az óra harmadik részében megismertük a Banach–Tarski-paradoxont, s arra is fény derült, ami valószínűleg sokak fantáziáját megmozgatja és kedélyét felborzolja, hogy még a demokrácia is lehetetlen...
T. B.

Címkék
Legolvasottabb
Portál
Rendezvénynaptár 
-
Karikó Katalin állandó kiállítás
június 30. - december 31. -
Részletes táblázatos nézet
augusztus 25. - július 12. -
2025/2026/1. féléves matrica átvétel
szeptember 08. - február 02. -
Kiállítás a Mérnöki Kar munkatársainak fotóiból
október 15. - december 19. -
Vizsgák meghirdetése
november 03. - február 04.


 Cikk nyomtatás
Cikk nyomtatás Link küldés
Link küldés Megosztás
Megosztás

